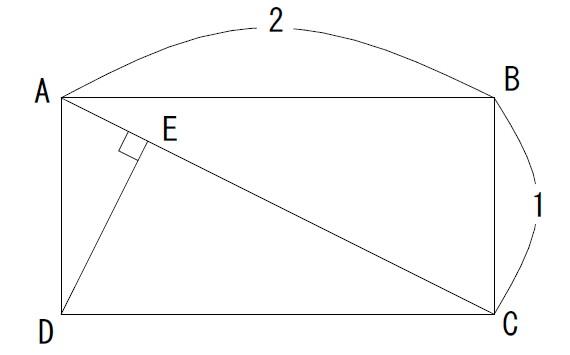
次の図のように、辺の長さの比が2 : 1 となっている長方形ABCDがある。この長方形ABCDに対角線ACを引き、AC上の点Eから頂点Dに垂線を引いたとき、三角形CDEの面積が、長方形ABCDに占める割合はどれか。
1 \(\frac{1}{10}\)
2 \(\frac{1}{5}\)
3 \(\frac{3}{10}\)
4 \(\frac{2}{5}\)
5 \(\frac{1}{2}\)

模擬面接、職務経験論文対策も万全、特別区経験者試験に向け充実のサポート体制。資料請求!
正答 4
三角形CDEと三角形DAE、三角形ACBは相似である。
したがってCE:DE=2:1,DE:AE=2:1だから
CE:AE=4:1
底辺分割定理より、三角形CDEの面積は三角形CDAの\(\frac{4}{5}\)
三角形CDAは長方形ABCDの\(\frac{1}{2}\)だから、三角形CDEは長方形ABCDの\(\frac{1}{2}×\frac{4}{5}=\frac{2}{5}\)
