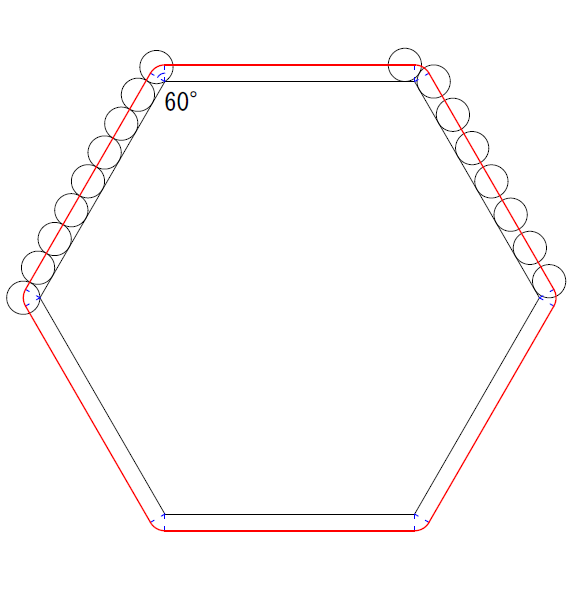
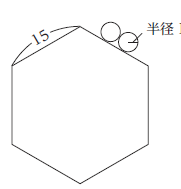
図のように,一辺の長さが15 の正六角形の板が1 枚と半径1 の円板が複数ある。正六角形の板の周りに半径1 の円板を次の条件を満たすように置いた場合,円板は最大で何枚並べることができるか。
○ 正六角形の板と円板,また,円板どうしは重ねて置くことはできない。
○ 全ての円板は,正六角形の板と1 点で接する(頂点で接していてもよい)。
1. 36
2. 40
3. 42
4. 44
5. 48

模擬面接、面接カード対策も万全、刑務官試験に向け充実のサポート体制。資料請求!
正答 5
いろいろな位置で円を六角形の外側に配置したとき、円の中心の軌跡は次の赤い線となる。
直線部分は\(15×6=90\)
角の部分は、半径\(1\),中心角\(60°\)の扇形(六角形の内角は120°)となるから、その長さの合計(扇形6個分)は\(2π\)である。したがって中心部分の軌跡の長さは\(90+2π\)
円の直径は2であるから、配置できる円の数は\(\frac{90+2π}{2}=45+π=48.14\)
円の個数は整数であるから、最大48個