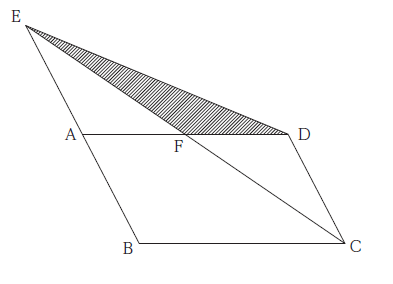
図のように、平行四辺形ABCD の、線分BA の延長上にAE =AB になるように点Eをとり、AD とCE の交点をF とする。三角形DEF(斜線部)の面積が2 であるとき、平行四辺形ABCD の面積はいくらか。
1. 6
2. 7
3. 8
4. 9
5. 10

模擬面接、面接カード対策も万全、刑務官試験に向け充実のサポート体制。資料請求!
正答3
AE=ABなのでAE=DCまた∠EAD=∠CDAだから、三角形DEFの面積と三角形DCFの面積は等しい。
三角形EBCにおいて中点連結定理より、AFはBCの半分なので、三角形DCFは平行四辺形ABCDの面積の4分の1である。
したがって、三角形DEFの面積を2とすると平行四辺形ABCDの面積は4倍の8となる。
