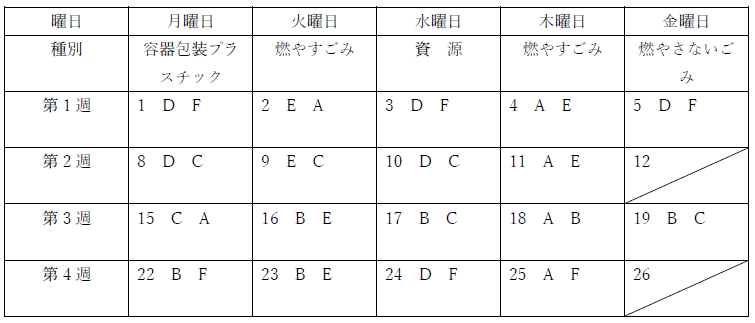
共同生活をしているA~Fの6 人が、次の表のように、月曜日から始まる4 週間分の資源とごみの当番表を作成することになった。この地域の収集日は、月曜日は容器包装プラスチック、火曜日と木曜日は燃やすごみ、水曜日は資源、第1 、第3 金曜日は燃やさないごみとなっている。今、2 人一組で各人が6 日ずつ、当番を担当するに当たり、A~Fの各人は、次のような要望を出している。これらの要望を全て満足するように当番表を作成したとき、確実にいえるのはどれか。
A 木曜日は全て担当したい。Dと組むことができないが、それ以外の人とは少なくとも1 回は組みたい。
B 第3 週の火曜日から6 回連続して担当したい。Dと組むことができない。
C 第2 週と第3 週に担当したい。
D 第3 週は担当できない。
E 燃やすごみの日だけ担当したい。Dと組むことができない。
F 第4 週に3 回担当したい。
1 Fは、金曜日を1 回担当する。
2 Dは、木曜日を2 回担当する。
3 Cは、水曜日を1 回担当する。
4 Bは、火曜日を1 回担当する。
5 Aは、月曜日を2 回担当する。
正答 1
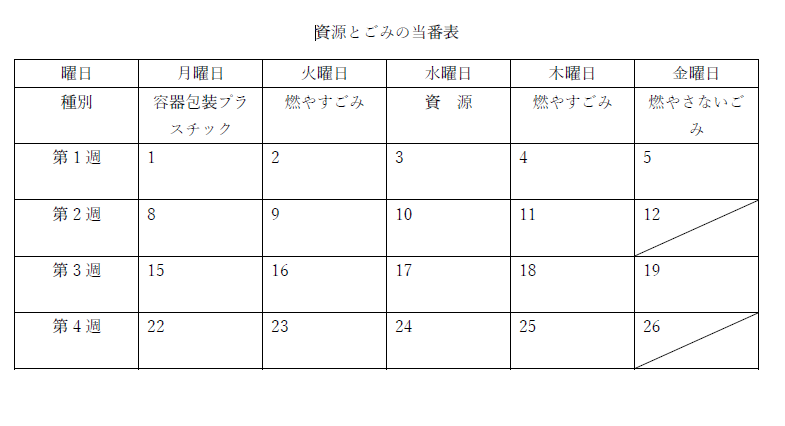
表にAとBの確実なところだけ記入する。
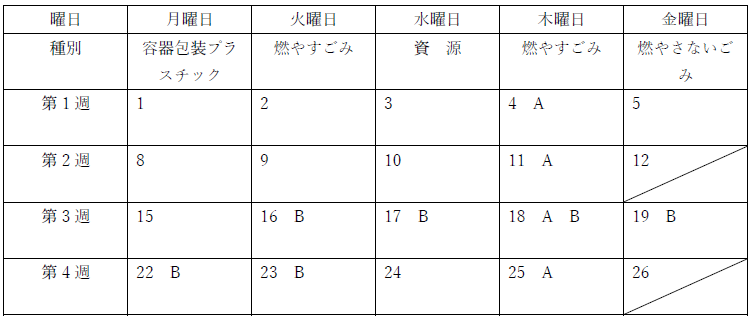
ここで、EとFについて考えると、Eは燃やすごみの日だけを担当したい、とある。空いているのは全部で7日間あるので、そのうちの6日間である。しかし、Fが第4週に3回担当したいとあるので、少なくともそのうちの1日は燃やすごみの日となりその日はEに割り振れないので、第1週から第3週までの燃やすごみの日には必ずEが入ることになる。残りの一日は23か25日である。
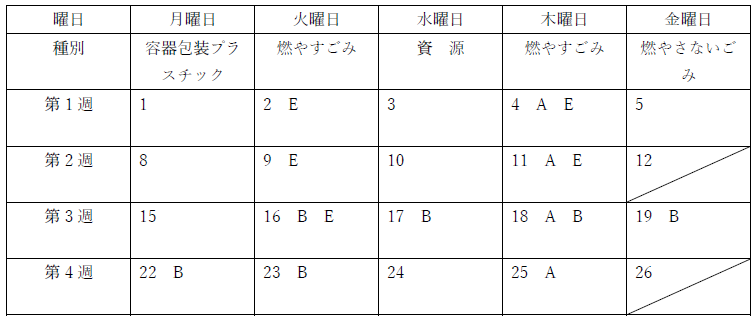
次にDの入るところを探すと、第3週には入らず、A、B、Eとも被らないので次のようになる。
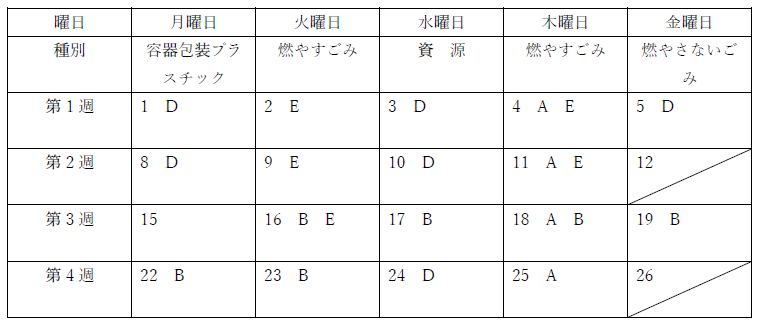
Cは第2週と第3週のみなので次のようになる。
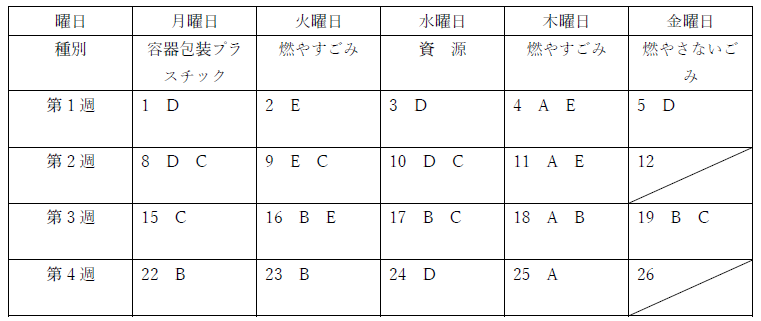
ぎにAとF、AとCの組み合わせを探すと、AとFは25日しかなく、AとCは15日しか入れられない。Eの残りの1日は23日となる。
すると、Fの第4週もきまる。
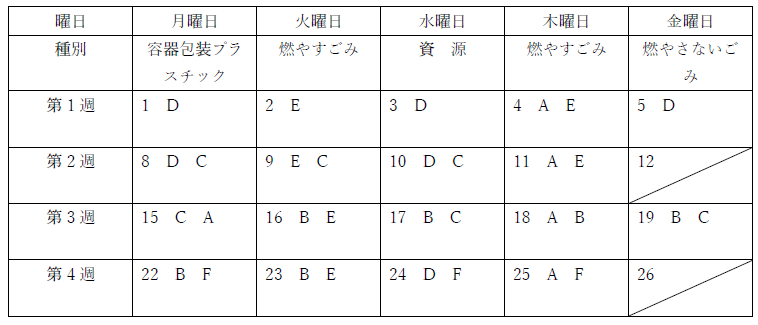
Aの残りの一日はDとは一緒にならないことより2日となり、Fの残りも確定する。